Historical Context
The three-body problem is a fundamental challenge in physics and astronomy: predicting the motion of three massive bodies (like planets or stars) under their mutual gravitational attraction. The problem traces back to Isaac Newton in the late 17th century, who developed the laws of motion and gravitation. Early attempts to understand the Moon's motion (lunar theory) and improve navigation led to intense study of the three-body problem, as the Sun, Earth, and Moon interact gravitationally.
In the 19th century, Henri Poincaré made breakthrough contributions, showing the system's inherent complexity and laying the foundations of chaos theory. The three-body problem has since inspired centuries of research, impacting mathematics, physics, and astronomy.
Mathematical Formulation
The three-body problem involves solving Newton's equations for three masses \((m_1, m_2, m_3)\) at positions \((\vec{r}_1, \vec{r}_2, \vec{r}_3)\):
where \(G\) is the gravitational constant. The system can also be described using the Hamiltonian formalism, which encapsulates the total energy (kinetic + potential) in a single function.
Special cases include the restricted three-body problem, where one mass is negligible (e.g., a spacecraft influenced by Earth and Moon), and symmetrical configurations like Lagrange points.
Significance in Physics and Astronomy
- Planetary Motion: Predicting the stability of planets and moons relies on understanding three-body (and more) interactions.
- Chaos Theory: The problem revealed how tiny changes in initial conditions can lead to vastly different outcomes.
- Space Missions: Accurate navigation requires accounting for the gravitational effects of multiple bodies.
- Exoplanets: Many discovered planetary systems are strongly shaped by multi-body gravitational dynamics.
Why Is the Three-Body Problem Analytically Unsolvable?
While the two-body problem (e.g., Sun and Earth) has a neat, closed-form solution (elliptical orbits), the three-body problem does not. Poincaré showed its solutions can be exceedingly complex and sensitive.
- Chaos: Tiny changes in initial conditions can cause wildly different outcomes.
- Sundman's Solution: A theoretical series solution exists but converges so slowly it's impractical.
- Special Cases: Only a handful of symmetric, restricted configurations (like Lagrange points) have closed-form solutions.
- Numerical Methods: Today, computers numerically integrate the equations to simulate real systems.
Visualizations
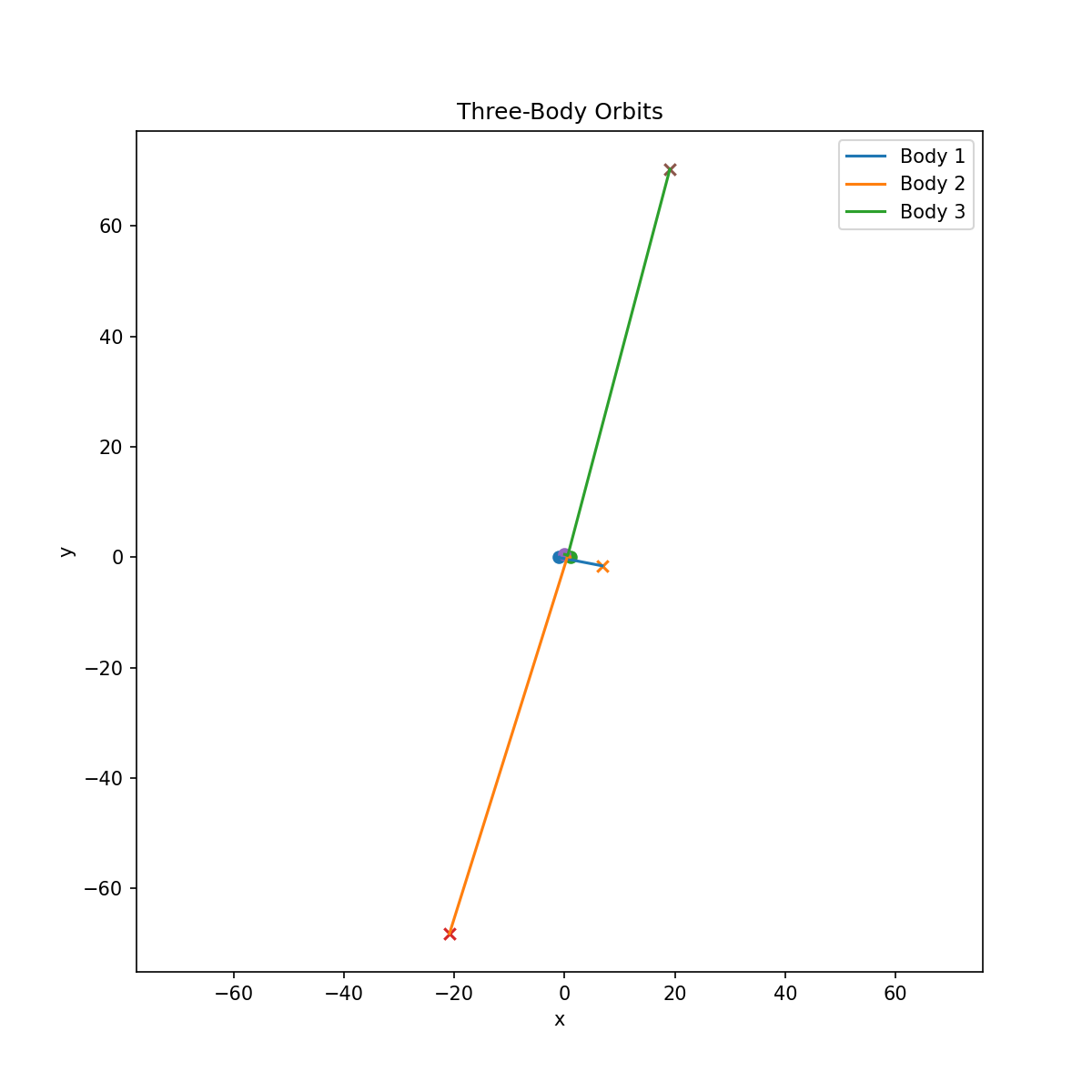
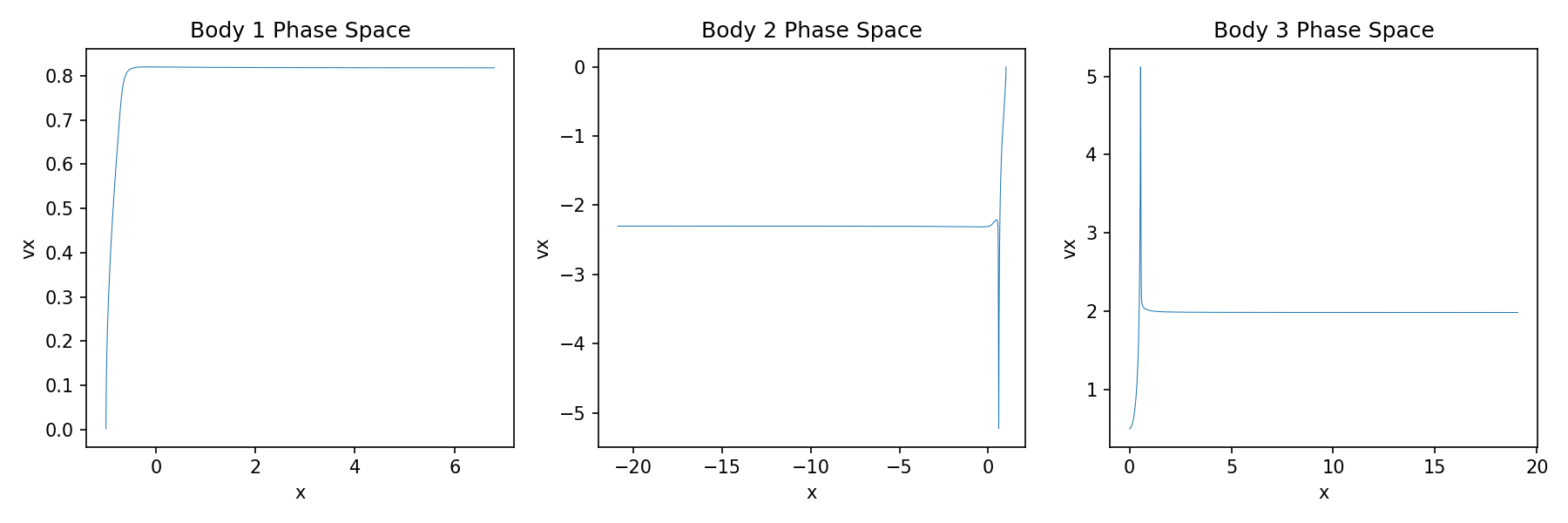
Animations
Figure-8 Orbit: A rare, periodic solution where three equal masses chase each other in a figure-8.
View animation on Wikipedia.
Chaotic Trajectories: Most three-body setups are chaotic.
View animation on Wikipedia.
Interactive Three-Body Simulation
How to Use the Simulation
- Select a preset or randomize to see different initial conditions.
- Drag the colored circles on the canvas to set starting positions.
- Click and drag the velocity arrows to adjust starting velocities.
- Control playback speed with the slider.
- Observe the resulting orbits and phase space plot.
- Reset to revert to the selected preset.
Chaos & Sensitivity to Initial Conditions
The three-body problem is a classic example of a chaotic system: small changes in starting positions or velocities can lead to dramatically different outcomes. Try adjusting the initial positions or velocities just slightly in the simulation above, or click "Randomize" multiple times — you'll often see completely new behaviors.